1.
(a) Omezené podmnožiny R
Definujte (zdola, shora) omezenou podmnožinu R. Zaved’te pojmy minimum, maximum, infimum, supremum množiny.
Vysvětlete rozdíly a vztahy mezi těmito pojmy, představte jejich vlastnosti a ilustrujte je vhodnými příklady a protipřílady.
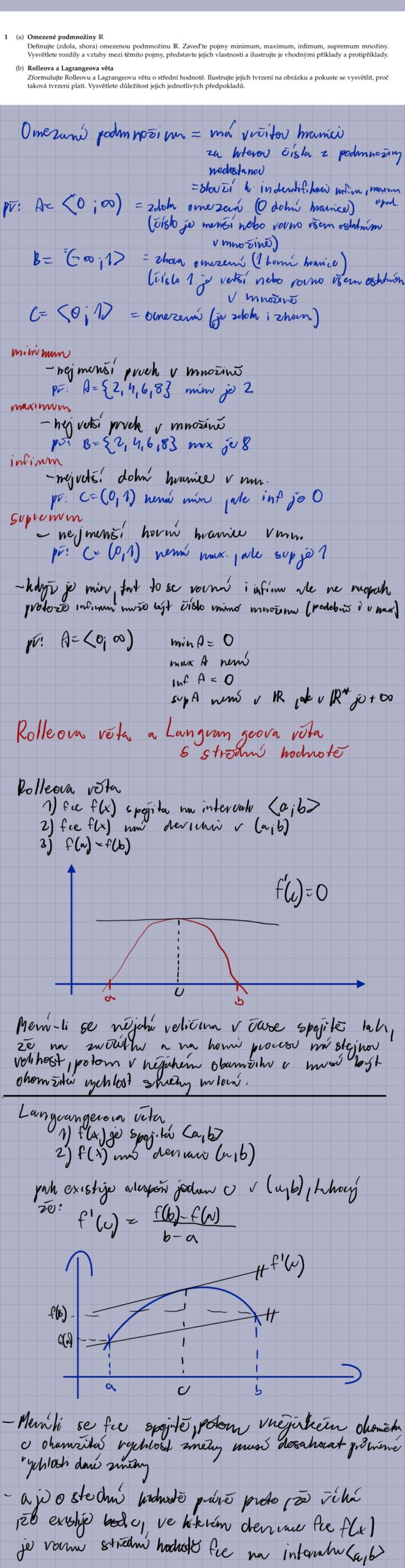
(b) Rolleova a Lagrangeova věta
Zformulujte Rolleovu a Lagrangeovu větu o střední hodnotě. Ilustrujte jejich tvrzení na obrázku a pokuste se vysvětlit, proč taková tvrzení platí. Vysvětlete důležitost jejich jednotlivých předpokladů.
2.
3.

4.

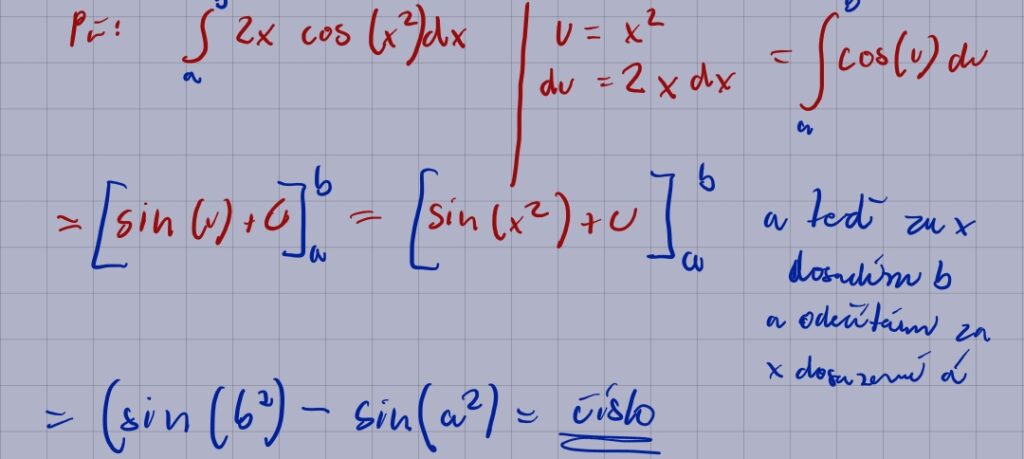
5.
Vysvětlete, na čem je založena metoda per partes při výpočtu neurčitého integrálu. Na příkladech ilustrujte, kdy je, resp. není vhodné ji použít. Vysvětlete, v čem tkví obtížnost integrování oproti derivování. Vysvětlete, jak funguje metoda per partes při výpočtu určitého integrálu.
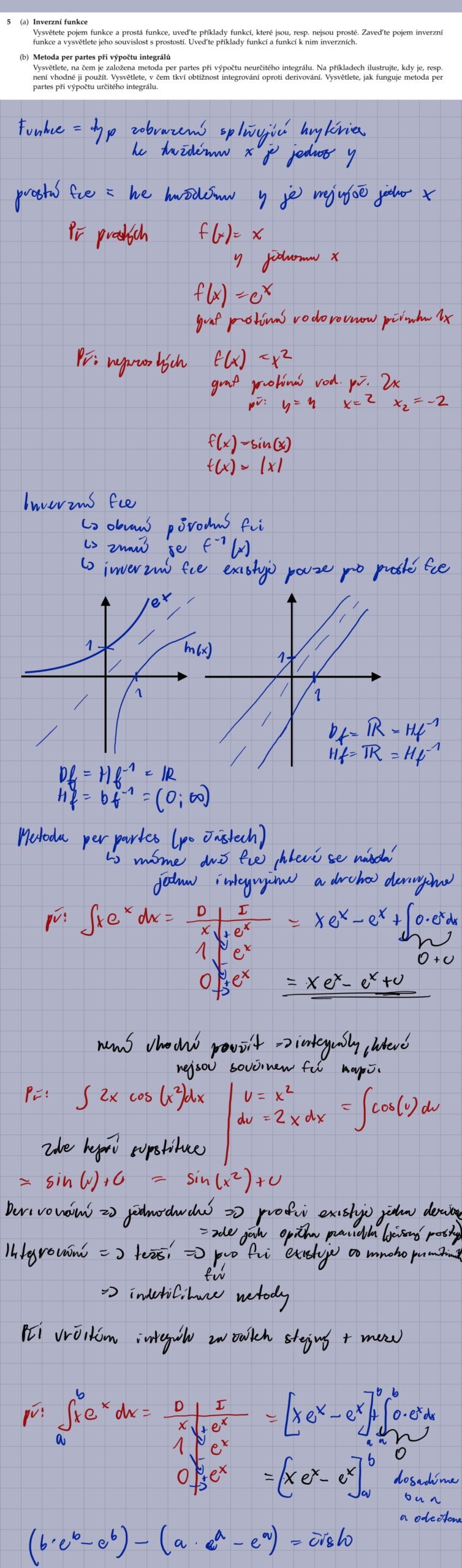
6.

7.
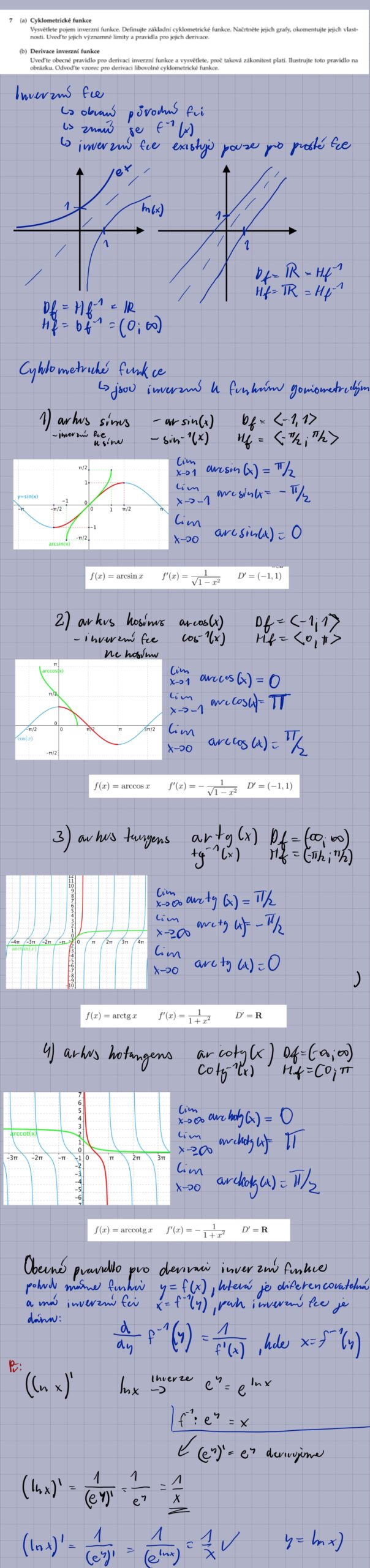
8.

9.
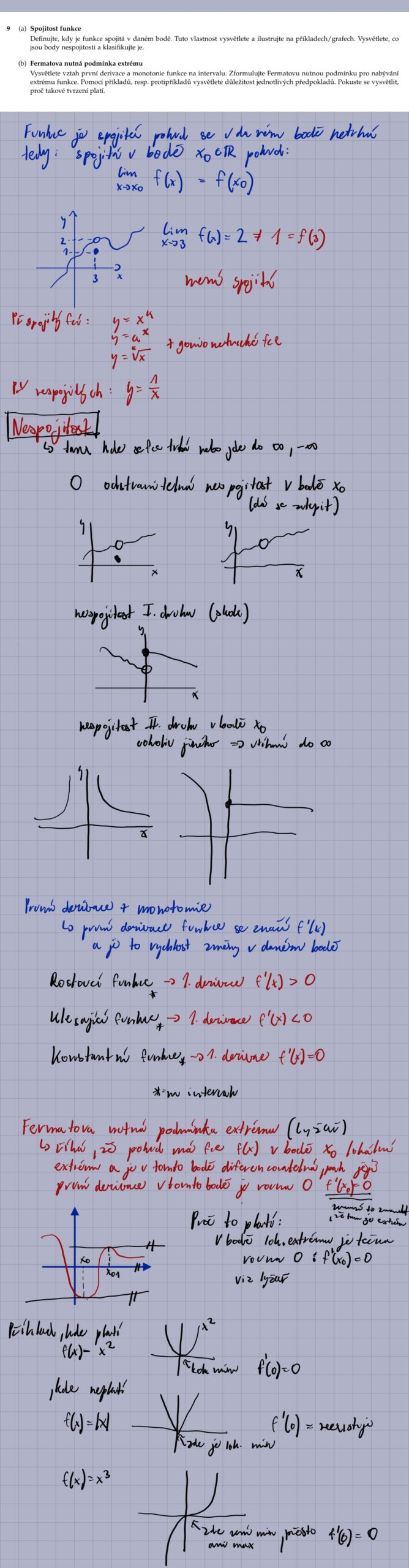
10.
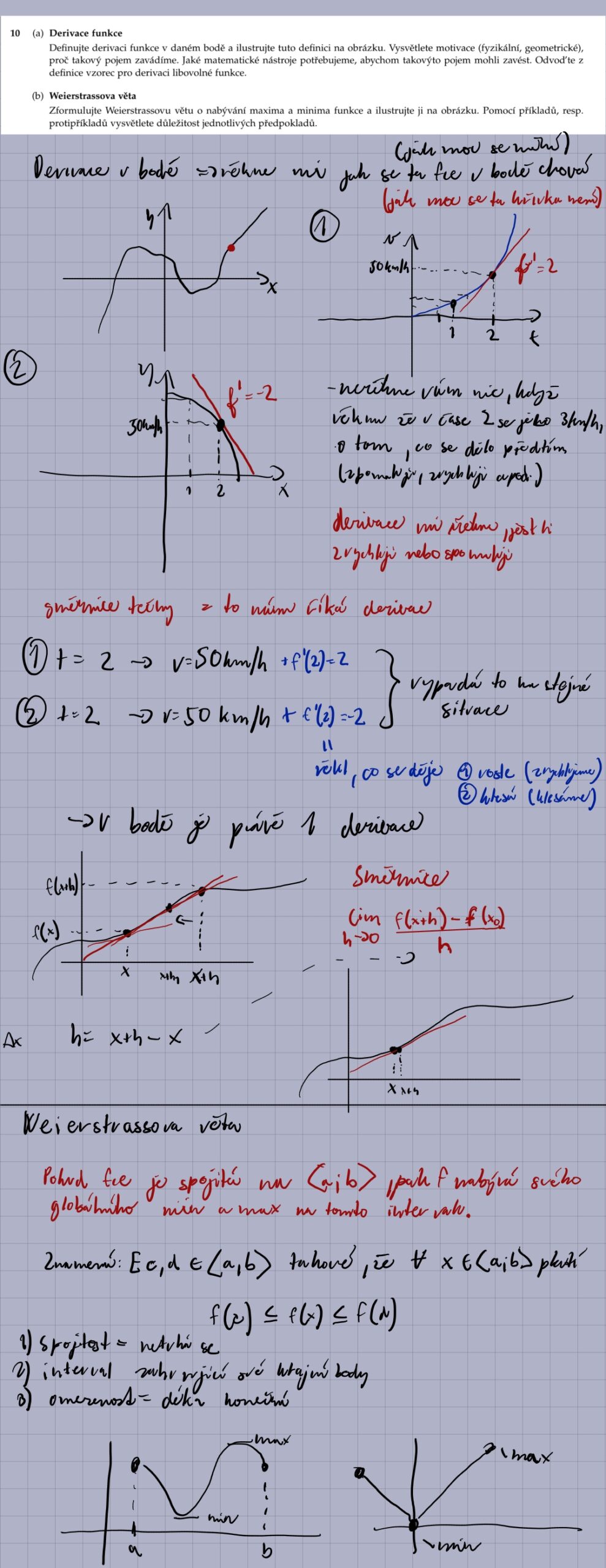
11.
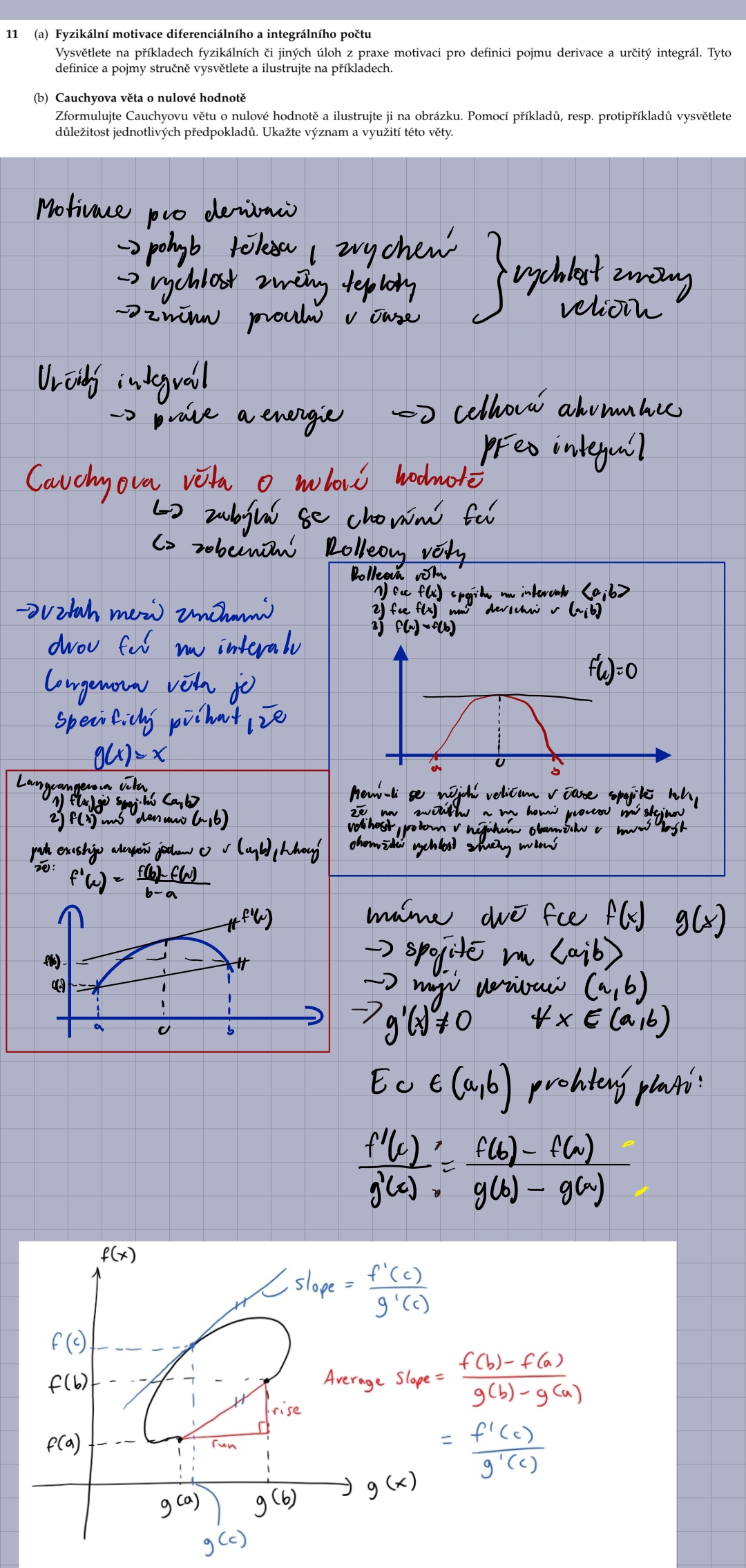
12.
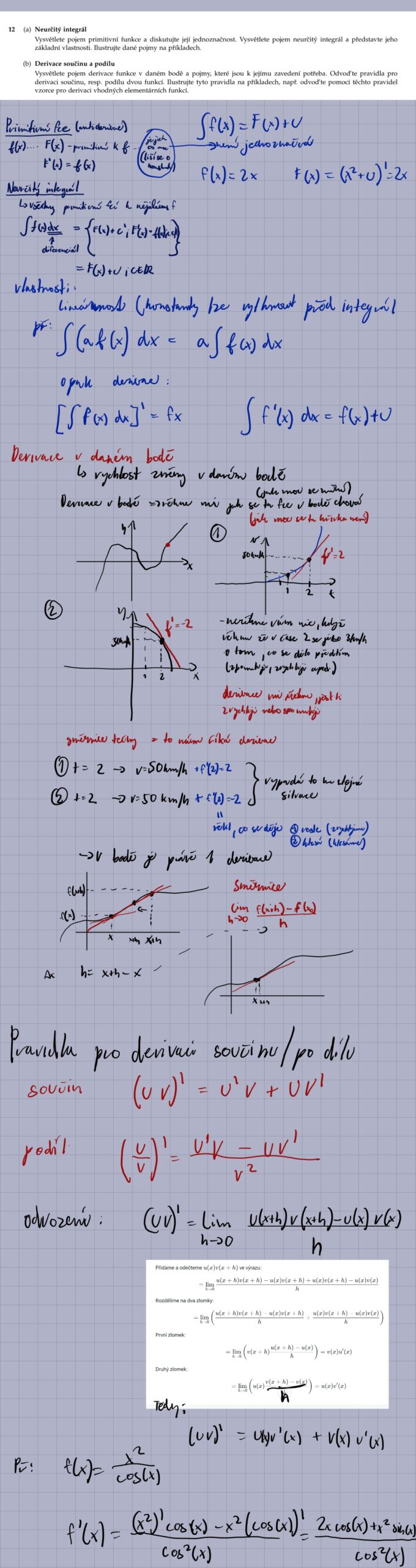
13.
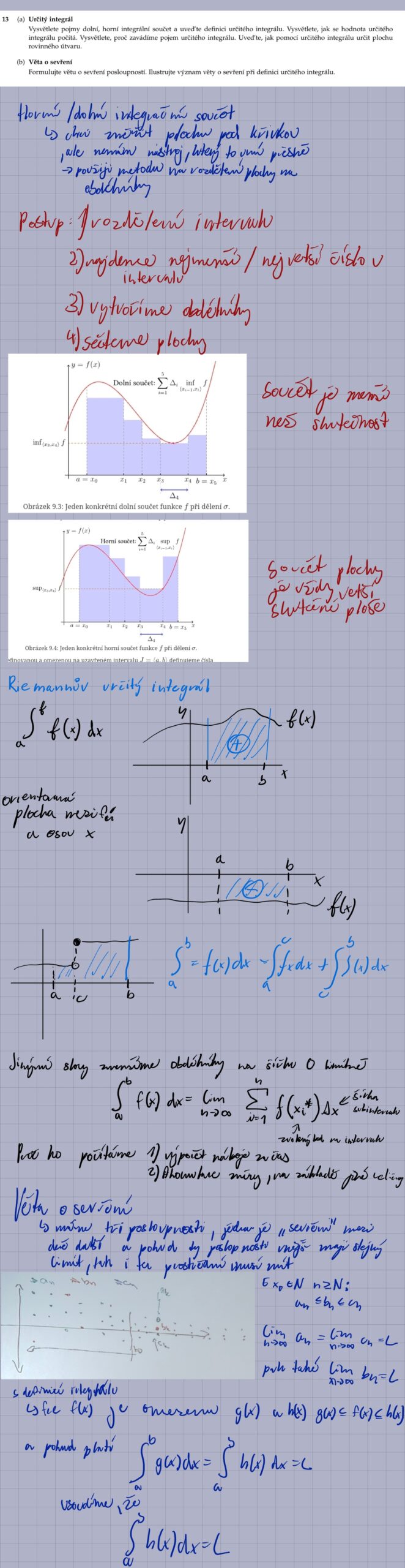
14.
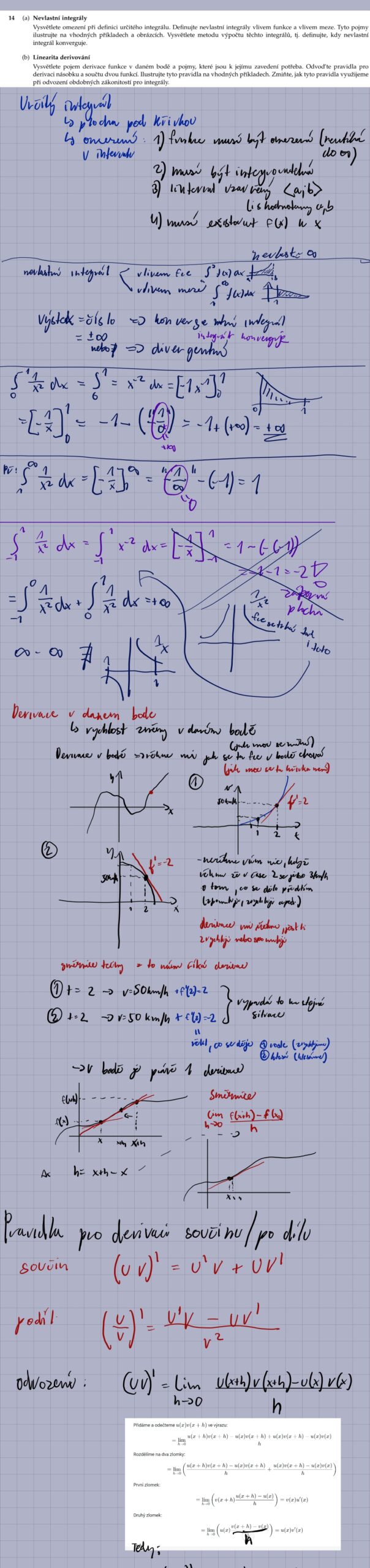
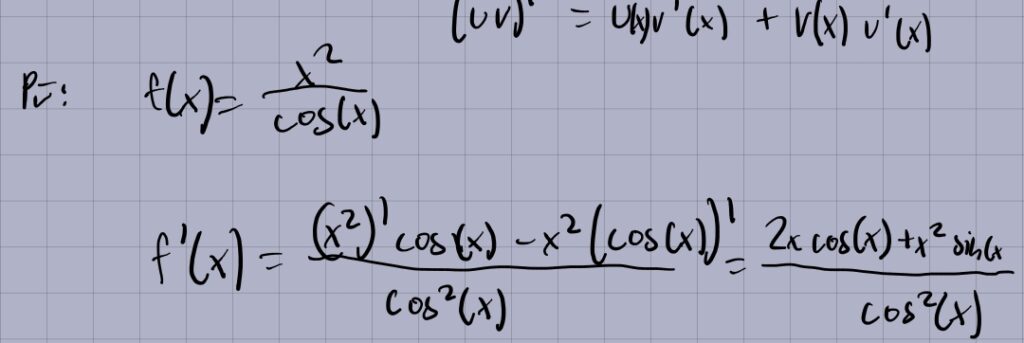
15.


Shrnutí
1. Jaké jsou rozdíly mezi minimem, maximem, infimem a supremem množiny, a jak je mohu ilustrovat?
Minimum množiny je nejmenší prvek množiny, maximum je největší prvek množiny. Minimum a maximum nemusí existovat (např. otevřený interval nemá minimum ani maximum). Infimum množiny je největší dolní závora množiny, a supremum je nejmenší horní závora množiny. Infimum a supremum existují vždy pro omezenou množinu reálných čísel. Ilustrace: Pro interval (0, 1) je infimum 0 a supremum 1, ale minimum a maximum neexistují. Pro množinu {1, 2, 3} je minimum 1, maximum 3, infimum 1 a supremum 3.
2. Vysvětlete Rolleovu a Lagrangeovu větu o střední hodnotě a proč jsou důležité předpoklady nezbytné.
Rolleova věta říká, že pokud je funkce spojitá na uzavřeném intervalu [a, b], diferencovatelná na otevřeném intervalu (a, b), a f(a) = f(b), pak existuje alespoň jeden bod c v (a, b) takový, že f'(c) = 0. Lagrangeova věta (věta o střední hodnotě) říká, že pokud je funkce spojitá na uzavřeném intervalu [a, b] a diferencovatelná na otevřeném intervalu (a, b), pak existuje alespoň jeden bod c v (a, b) takový, že f'(c) = (f(b) – f(a))/(b – a). Předpoklady jsou důležité, protože pokud funkce není spojitá nebo diferencovatelná, nemusí věty platit. Například, pokud funkce není spojitá, nemusí existovat bod, kde derivace odpovídá průměrné změně funkce.
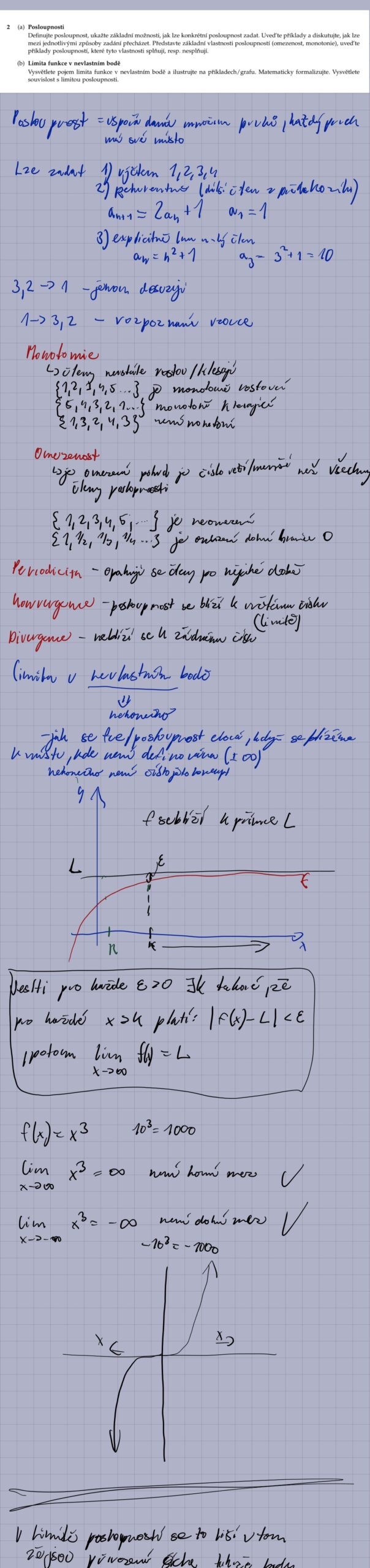
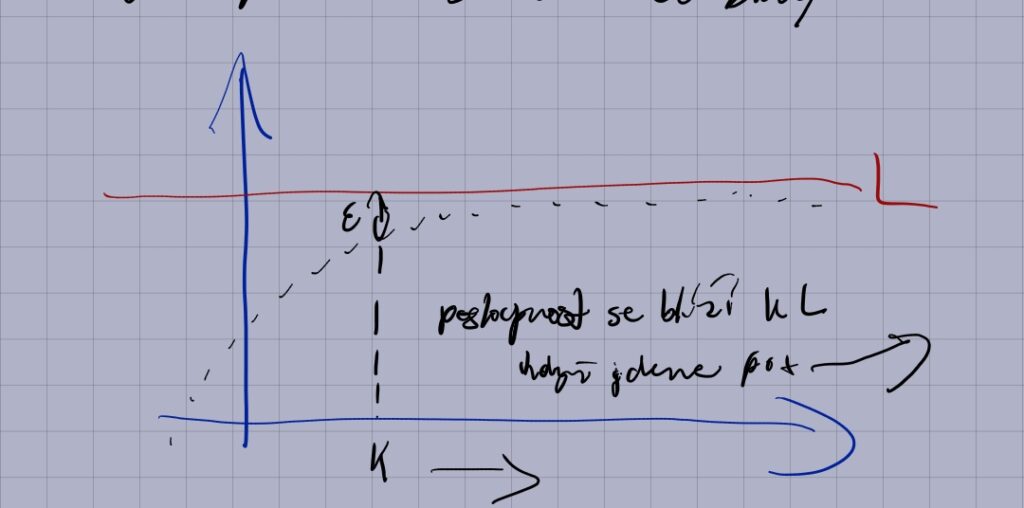
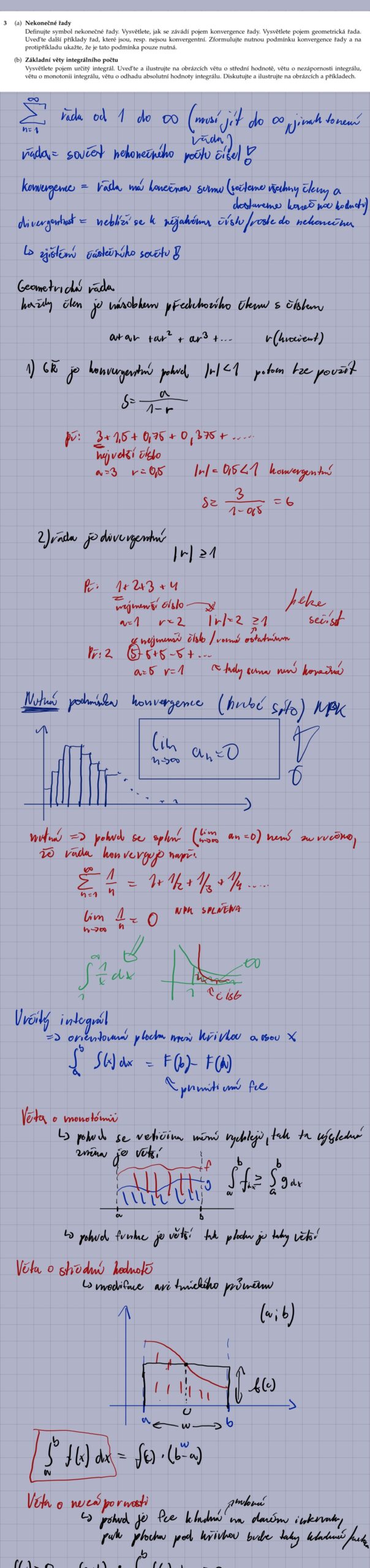
3. Co je to nekonečná řada a jak zjistím, zda konverguje? Jaká je nutná podmínka konvergence?
Nekonečná řada je součet nekonečně mnoha členů. Řada konverguje, pokud posloupnost částečných součtů konverguje k určité limitě. Geometrická řada je příkladem řady, kterou lze snadno analyzovat. Nutná podmínka konvergence řady Σ a_n je, že lim_{n→∞} a_n = 0. To znamená, že členy řady se musí blížit k nule. Tato podmínka je pouze nutná, ale ne postačující. Příkladem je harmonická řada Σ 1/n, kde lim_{n→∞} 1/n = 0, ale řada diverguje.
4. Jak funguje substituční metoda pro výpočet neurčitého a určitého integrálu, a kdy je vhodné ji použít?
Substituční metoda je založena na řetězovém pravidle derivování. Spočívá v tom, že se zvolí vhodná substituce u = g(x), vypočítá se du = g'(x) dx, a integrál se přepíše do podoby ∫ f(g(x))g'(x) dx = ∫ f(u) du. Substituční metoda je vhodná, pokud integrand obsahuje funkci a její derivaci (až na konstantu). U určitého integrálu je nutné při substituci změnit i meze integrálu: pokud původně integrujeme od a do b, a u = g(x), pak nové meze jsou g(a) a g(b).
5. Vysvětlete metodu per partes pro výpočet integrálů a jak ji aplikovat na určité integrály.
Metoda per partes je založena na pravidlu pro derivaci součinu. ∫ u dv = uv – ∫ v du. Volba u a dv je klíčová. Snažíme se vybrat u tak, aby se jeho derivací zjednodušil integrál. U určitého integrálu se aplikuje vzorec: ∫ₐᵇ u dv = [uv]ₐᵇ – ∫ₐᵇ v du. Tedy, je třeba dosadit meze do členu uv.
6. Definujte cyklometrické funkce a uveďte příklady jejich derivací.
Cyklometrické funkce jsou inverzní funkce k goniometrickým funkcím. Patří sem arcsin(x), arccos(x), arctan(x) a arccot(x). Jejich grafy vznikají zrcadlením grafů goniometrických funkcí podle osy y = x a omezením definičního oboru goniometrických funkcí, aby byly prosté. Příklady derivací: d/dx arcsin(x) = 1/√(1 – x²) a d/dx arctan(x) = 1/(1 + x²).
7. Co je l’Hôpitalovo pravidlo a kdy ho můžu použít? Jaké jsou jeho silné a slabé stránky?
L’Hôpitalovo pravidlo se používá k výpočtu limit neurčitých výrazů typu 0/0 nebo ∞/∞. Pravidlo říká, že pokud lim_{x→c} f(x) = 0 a lim_{x→c} g(x) = 0 (nebo obě limity jsou ∞), a lim_{x→c} f'(x)/g'(x) existuje, pak lim_{x→c} f(x)/g(x) = lim_{x→c} f'(x)/g'(x). Síla: Efektivní pro výpočet limit složitých výrazů. Slabá stránka: Je třeba ověřit, že limity derivací existují a že se jedná o neurčitý výraz správného typu. Někdy je třeba pravidlo použít opakovaně.
8. Jaký je rozdíl mezi spojitostí a diferencovatelností funkce v daném bodě?
Funkce je spojitá v bodě, pokud limita funkce v tomto bodě existuje a rovná se funkční hodnotě v tomto bodě. Funkce je diferencovatelná v bodě, pokud existuje derivace funkce v tomto bodě. Diferencovatelnost implikuje spojitost, ale spojitost neimplikuje diferencovatelnost. Například funkce |x| je spojitá v bodě x = 0, ale není v tomto bodě diferencovatelná (má ostrou hranu).
- Co jsou to omezené podmnožiny R? Omezená podmnožina R zdola má dolní závoru, tedy existuje číslo, které je menší nebo rovno všem prvkům množiny. Omezená podmnožina R shora má horní závoru, existuje číslo, které je větší nebo rovno všem prvkům množiny.
- Formulujte Rolleovu větu o střední hodnotě. Rolleova věta říká, že pokud je funkce spojitá na uzavřeném intervalu [a, b], diferencovatelná na otevřeném intervalu (a, b) a f(a) = f(b), pak existuje bod c v (a, b) takový, že f'(c) = 0.
- Jak lze zadat posloupnost? Uveďte možnosti. Posloupnost lze zadat explicitním vzorcem, rekurentním vzorcem (kde n-tý člen je definován pomocí předchozích členů), nebo výčtem prvků (pokud je posloupnost konečná).
- Vysvětlete pojem limita funkce v nevlastním bodě. Limita funkce v nevlastním bodě popisuje chování funkce, když se její argument blíží k nekonečnu (kladnému nebo zápornému). Formálně to znamená, že pro libovolně malé okolí limity existuje dostatečně velké číslo, za kterým se funkční hodnoty nacházejí v daném okolí.
- Definujte konvergenci nekonečné řady. Nekonečná řada konverguje, pokud existuje konečná limita posloupnosti částečných součtů. To znamená, že součet prvních n členů řady se s rostoucím n blíží k určité hodnotě.
- Uveďte větu o monotonii integrálu. Věta o monotonii integrálu říká, že pokud f(x) ≤ g(x) pro všechna x v intervalu [a, b], pak integrál f(x) od a do b je menší nebo roven integrálu g(x) od a do b.
- Co jsou D(f) a H(f)? D(f) značí definiční obor funkce f, tedy množinu všech hodnot, pro které je funkce definována. H(f) značí obor hodnot funkce f, tedy množinu všech hodnot, kterých funkce nabývá.
- Popište základní princip substituční metody při výpočtu neurčitého integrálu. Substituční metoda spočívá v zavedení nové proměnné, která zjednoduší integrovanou funkci. Cílem je transformovat integrál na tvar, který lze snadněji vypočítat pomocí známých integračních vzorců.
- Co je to prostá funkce a jaký je její vztah k inverzní funkci? Prostá funkce je taková funkce, kde každé dvě různé hodnoty z definičního oboru mají různé funkční hodnoty. Prostá funkce má inverzní funkci, která „vrací“ původní hodnotu.
- Zformulujte l’Hôpitalovo pravidlo. L’Hôpitalovo pravidlo se používá pro výpočet limit neurčitých výrazů typu 0/0 nebo ∞/∞. Pravidlo říká, že limita podílu dvou funkcí se rovná limitě podílu jejich derivací, pokud existuje.
- Omezená podmnožina R zdola má dolní závoru, tedy existuje číslo, které je menší nebo rovno všem prvkům množiny. Omezená podmnožina R shora má horní závoru, existuje číslo, které je větší nebo rovno všem prvkům množiny.
- Rolleova věta říká, že pokud je funkce spojitá na uzavřeném intervalu [a, b], diferencovatelná na otevřeném intervalu (a, b) a f(a) = f(b), pak existuje bod c v (a, b) takový, že f'(c) = 0.
- Posloupnost lze zadat explicitním vzorcem, rekurentním vzorcem (kde n-tý člen je definován pomocí předchozích členů), nebo výčtem prvků (pokud je posloupnost konečná).
- Limita funkce v nevlastním bodě popisuje chování funkce, když se její argument blíží k nekonečnu (kladnému nebo zápornému). Formálně to znamená, že pro libovolně malé okolí limity existuje dostatečně velké číslo, za kterým se funkční hodnoty nacházejí v daném okolí.
- Nekonečná řada konverguje, pokud existuje konečná limita posloupnosti částečných součtů. To znamená, že součet prvních n členů řady se s rostoucím n blíží k určité hodnotě.
- Věta o monotonii integrálu říká, že pokud f(x) ≤ g(x) pro všechna x v intervalu [a, b], pak integrál f(x) od a do b je menší nebo roven integrálu g(x) od a do b.
- D(f) značí definiční obor funkce f, tedy množinu všech hodnot, pro které je funkce definována. H(f) značí obor hodnot funkce f, tedy množinu všech hodnot, kterých funkce nabývá.
- Substituční metoda spočívá v zavedení nové proměnné, která zjednoduší integrovanou funkci. Cílem je transformovat integrál na tvar, který lze snadněji vypočítat pomocí známých integračních vzorců.
- Prostá funkce je taková funkce, kde každé dvě různé hodnoty z definičního oboru mají různé funkční hodnoty. Prostá funkce má inverzní funkci, která „vrací“ původní hodnotu.
- L’Hôpitalovo pravidlo se používá pro výpočet limit neurčitých výrazů typu 0/0 nebo ∞/∞. Pravidlo říká, že limita podílu dvou funkcí se rovná limitě podílu jejich derivací, pokud existuje.
